Log-normal-fordelingen
Den fordeling som gennemgås på denne side, er primært relevant i forbindelse med bestemmelsen af referenceintervaller. Det kan derfor være en fordel at vente med at læse denne side, indtil man har læst om referenceintervaller i kapitel 4.
I forbindelse med biologisk variation ses ofte en anden fordeling (end normalfordelingen), nemlig den såkaldte log-normal-fordeling. Denne fordeling er karakteriseret ved, at hvis man tager logaritmen til tal fra fordelingen, så fås tal der er normalfordelt. Dette kan udnyttes til at beregne fraktiler og sandsynligheder i fordelingen, hvilket ofte anvendes i forbindelse med fastlæggelse af referenceintervaller.
Fordelingen
Histogrammet for en log-normalt-fordelt population ser som vist på figur 1 herunder, dvs. at den har en "hale" af høje værdier. Det tilhørende qq-plot er vist i figur 2. Her skal man bemærke at qq-plottet buer opad.
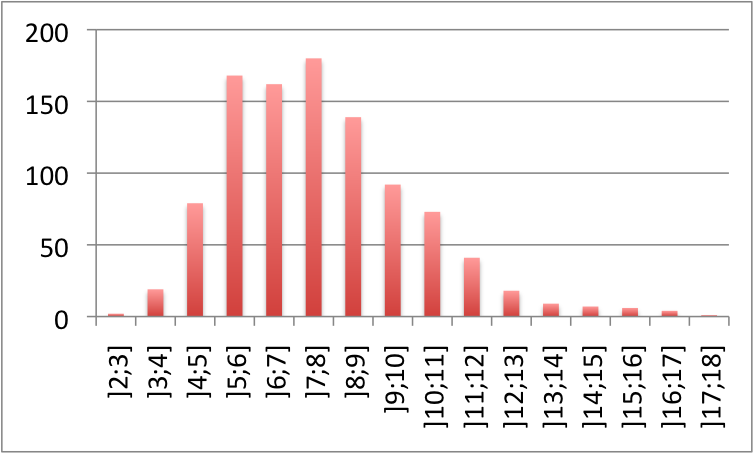
Figur 1: Et histogram for en tilfældig log-normal-fordeling.
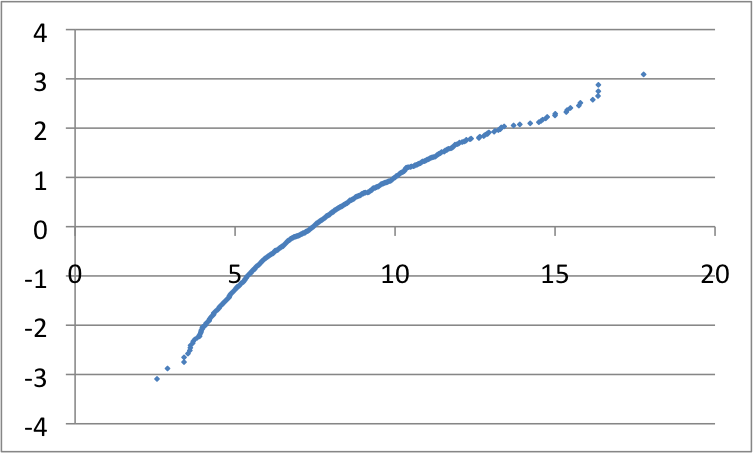
Figur 2: qq-diagram svarende til histogrammet ovenfor.
Det der er helt afgørende for om der er tale om en log-normal fordeling, er imidlertid om qq-plottet bliver til en ret linie hvis man først tager logaritmen til alle tallene.
Beregning af fraktiler
Hvis man har afgjort at man har en stikprøve der stammer fra en log-normal-fordelt population, så kan man bestemme en vilkårlig p-fraktil i fordelingen efter følgende opskrift:
- Tag logaritmen til alle tal i fordelingen - det er lige meget om man anvender 10-tals logaritmen eller den naturlige logaritme. Dvs. transformer log-normal-fordelingen til en normal-fordeling.
- Man har nu en normalfordelt stikprøve. Beregn middelværdi og spredning for denne stikprøve.
- Bestem den ønskede fraktil for den transformerede fordeling, som beskrevet på side 3.12.
- Transformer denne værdi tilbage til den oprindelige fordeling, ved at bruge den inverse funktion til den logaritmefunktion der blev anvendt i punkt 1. Hvis man anvendte 10-talslogaritmen, hvis x er den beregnede fraktil i normalfordelingen og hvis y er den ønskede fraktil i log-normal-fordelingen, så er formlen altså:
$$ y =10^x$$
Hvis man i stedet har anvendt den naturlige logaritme, skal 10 udskiftes med e.
Eksempel
Betragt de 200 tal der findes i dette regneark. Tallene er P-bilirubin, stofk. fra det nordiske referenceinterval projekt. I dette eksempel ønskes en beregning af 0,025-fraktilen i den fordeling der beskriver P-bilirubin, stofk.
Hvis man fremstiller et qq-plot af disse tal, ser det ud som vist her:

Der ses tydeligt at diagrammet buer opad, hvilket indikerer en log-normal-fordeling. Bemærk at hvis man anvender software som har en indbygget funktion til at fremstille qq-plot, er det ikke sikkert at de observerede værdier afbildes på x-aksen. Hvis man i stedet har de observerede på y-aksen og de teoretiske fraktiler på x-aksen, så kommer grafen naturligvis til at bue "nedad" i stedet.
Hvis man synes at qq-plottet derfor er lidt forvirrende, kan det være enklere at det tilhørende histogram, og observere at det har en hale af høje værdier.
Tager man nu logaritmen til alle tallene, og fremstiller et nyt qq-plot, ser det ud som vist her (i dette tilfælde er den naturlige logaritme anvendt):

Da dette qq-plot ikke afviger væsentligt fra en ret linie, kan man nu tillade sig at antage, at der er tale om en log-normal-fordeling.
Man kan nu bestemme 0,025-fraktilen i stikprøven bestående af de transformerede værdier. Dette gøres ved at bestemme middelværdi og spredning, og bruge formlen fra side 3.12. Dette giver:
$$\overline{x} = 2{,}25 { }$$
$$SD = 0{,}39$$
$$0{,}025-fraktil = \overline{x} - 1{,}96\cdot SD = 1{,}49$$
Denne værdi skal nu transformeres tilbage til den oprindelige fordeling, som jo er den man er interesseret i. Dermed fås
$$0{,}025-fraktil \text{ (P-bilirubin)} = \exp(1{,}49) = 4{,}43\ \mu\text{mol/L}$$
Bemærk at man ikke uden videre kan transformere middelværdien og spredningen. Det er således kun fraktiler (herunder medianen) det giver mening at transformere frem og tilbage.
Bemærk desuden at man ikke kan tage logaritme og eksponential-funktionen til tal med en enhed. I forbindelse med transformationen er det derfor nødvendigt at fjerne enheden, og så tilføje den igen, når man transformerer tilbage. Tallene fra den transformerede fordeling ovenfor, er derfor opskrevet uden nogen enhed. |