t-test med 1 stikprøve
Formål
Formålet med denne test er at sammenligne middelværdien af èn population med en kendt værdi. Et typisk eksempel er kontrol af et apparats korrekthed (bias). Dette gøres ved at anvende en kontrolprøve med en kendt koncentration (eller som minimum hvor man har vedtaget en koncentration). Denne kontrolprøve analyseres så et antal gange, og man kan nu bruge en t-test til at undersøge om middelværdien af disse analyseresultater afviger signifikant fra prøvens sande (vedtagne) værdi.
Denne undersøgelse kan også foretages ved at beregne et konfidensinterval ud fra målingerne, og så se om den sande (vedtagne) værdi befinder sig i dette interval. Hvis man kigger lidt på formlerne, vil man se at det giver præcist samme resultat.
Forudsætninger og notation
En forudsætning for anvendelsen af denne test, er at stikprøven kan antages at stamme fra en normalfordeling. I ovennævnte eksempel er dette ikke noget problem, da det kun involverer analytisk variation, som stort set altid giver anledning til normalfordelte data. Antal målinger i stikprøven benævnes \(n\), stikprøvens middelværdi benævnes \(\overline{x}\), og populationens middelværdi benævnes \(\mu\). Populationens middelværdi ønskes sammenlignet med en kendt værdi, som benævnes \(\mu_0\). Den spredning der anvendes benævnes SD.
Fremgangsmåde
Først opskrives hypoteserne:
\(H_0:\mu=\mu_0\)
\(H_1:\mu\neq\mu_0\)
Disse hypoteser specificerer de to muligheder, man ønsker at hypotesetesten skal skelne mellem. I dette tilfælde er den ene mulighed, at populationens middelværdi (\(\mu\)) er identisk med den "kendte" værdi (\(\mu_0\)). Denne hypotese kaldes nul-hypotesen. Den anden mulighed er, at populationens middelværdi (\(\mu\)) er forskellig fra den "kendte" værdi (\(\mu_0\)). Denne hypotese kaldes modhypotesen.
Modhypotesen kan nogen gange sige at den ene middelværdi er større end den anden (læs mere herom på side 6.13), men nulhypotesen siger altid at middelværdierne er identiske.
Efter at have specificeret hypoteserne beregnes test-størrelsen efter formlen:
\[\begin{equation}\label{ref1}
t=\frac{\overline{x}-\mu_0}{SD/\sqrt{n}}
\end{equation}
\]
Bemærk at det der står under den øverste brøkstreg, er SEM (altså usikkerheden på middelværdien - genlæs eventuelt side 5.2). Dvs. \(t\) angiver hvor meget stikprøvens gennemsnit afviger fra den sande værdi, udtrykt i forhold til usikkerheden på gennemsnittet. Det er klart at hvis dette tal er stort, så tyder det på at afvigelsen er signifikant, hvorimod en lille værdi indikerer at afvigelsen kan forklares alene ud fra den tilfældige varition.
Ud fra t-værdien beregnes p-værdien (test-sandsynligheden). Princippet bag denne beregning er beskrevet på side 6.6, men gentages her. Til beregningen skal man bruge et antal frihedsgrader, som er beskrevet i sidste afsnit på denne side.
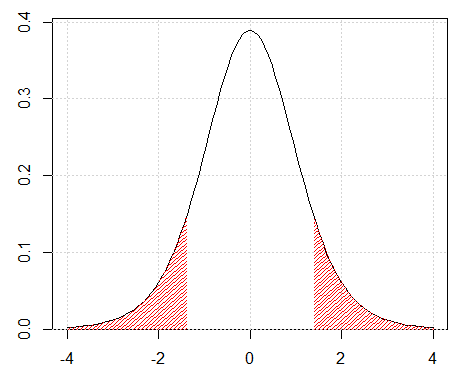
t-fordeling. Arealet under kurven er skraveret for \(t<-1{,}4\) og \(t>1{,}4\)
Hvis man har beregnet en t-værdi på f.eks. 1,4, så er p-værdien lig med det skraverede areal på ovenstående figur. Dvs. at p-værdien er lig med sandsynligheden for (hvis man gentager forsøget, og nulhypotesen er korrekt) at man får en t-teststørrelse som er mindre end -1,4 eller større end 1,4. Konkret foretages beregningen nemmest i Excel som vist på side 13.5.
Når p-værdien er beregnet konkluderes som beskrevet på side 6.6. Typisk vælger man et signifikansniveau på 5%, dvs. at:
\[\begin{align}
p>0{,}05 &\Rightarrow H_0 \text{ accepteres}\\
p<0{,}05 &\Rightarrow H_0 \text{ forkastes}\nonumber
\end{align}\]
Frihedsgrader
Bemærk at den spredning (SD) som bruges i formlen kan beregnes vha. tallene i stikprøven. I så fald er antallet af frihedsgrader (f) som bruges til beregning af p-værdien lig med n-1 (se side 4.11). Den kan imidlertid også være kendt fra andre sammenhænge. Et typisk eksempel er, at analyseusikkerheden kan beregnes fra mange måneders kontroller, mens middelværdien stadig beregnes fra et begrænset antal målinger - her sættes f i praksis til uendelig. |