Beregning af konfidensintervaller
Bemærk at nedenstående formel kun er gyldig for en normalfordelt population. Hvis antallet af målinger er tilpas stort, kan den sandsynligvis med rimelighed også anvendes selv om fordelingen afviger fra en normalfordeling. Men præcis hvad der er et tilpas stort antal er svært at sige noget generelt om (især fordi det bla. afhænger af hvor meget og hvordan målingerne afviger fra en normalfordeling).
Formlen til beregning af et 95%-konfidensinterval for middelværdien i en normalfordelt population er:
\[\begin{equation}
\textit{95%-konfidensinterval}=\left[\overline{x}-t_{0{,}975}(f)\cdot \frac{SD}{\sqrt{n}};\overline{x}+t_{0{,}975}(f)\cdot \frac{SD}{\sqrt{n}}\right]
\end{equation}\]
I det følgende gennemgås betydningen af de forskellige størrelser der indgår i formlen. Bemærk først at konfidensintervallet "udtaler" sig om den sande middelværdi for en population, men at man selvfølgelig anvender en stikprøve til at beregne konfidensintervallet.
- \(\overline{x}\) angiver selvfølgelig stikprøvens gennemsnit, og er således det bedste gæt på populationens middelværdi, når man tager udgangspunkt i stikprøven. (En anden stikprøve ville naturligvis give et andet gæt på populationens middelværdi).
- \(SD\) angiver stikprøvens spredning.
- \(n\) angiver det er antal målinger der er brugt til at bestemme gennemsnittet (\(\overline{x}\)).
- \(f\) er antallet af frihedsgrader hørende til spredningen (SD). Denne størrelse afhænger altså af hvordan \(SD\) er bestemt, og beregnes som forklaret på side 4.11.
- \(t_{0{,}975}(f)\) er 0,975-fraktilen i t-fordelingen med \(f\) frihedsgrader (beregnes som beskrevet på side 13.5). Ønsker man at fremstille et 90%-konfidensinterval, skal man bruge 0,95-fraktilen osv.
SEM
Størrelsen \(\frac{SD}{\sqrt{n}}\) kaldes ofte "Standard Error of Mean" (forkortes SEM), altså noget i stil med "usikkerhed på middelværdien", eller "standardfejl" (som blev introduceret kort på side 2.9). Ligesom enhver måling der kommer fra et apparat er behæftet med en usikkerhed, så er en bestemmelse af middelværdien naturligvis også, og denne usikkerhed kan beregnes som \(SEM=\frac{SD}{\sqrt{n}}\).
Denne formel har følgende (ikke overraskende) konsekvenser:
-
Jo større usikkerhed der er på den enkelte måling, jo større usikkerhed bliver der på gennemsnittet.
-
Jo flere målinger man anvender til at beregne gennemsnittet, jo mindre bliver usikkerheden på dette. Hvis man anvender 16 målinger bliver usikkerheden på gennemsnittet halvt så stor, som hvis man kun anvender 4 målinger.
- Figur 1 illustrerer sammenhængen mellem antallet af målinger og usikkerheden på gennemsnittet:
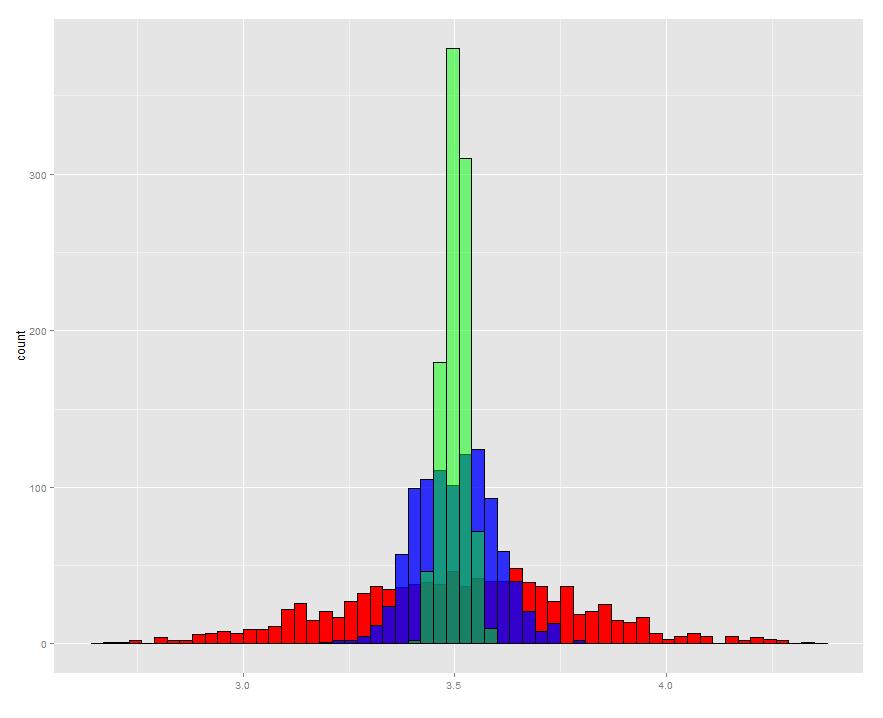
Figur 1: Rød: Fordeling af 1000 målinger med middelværdi 3,5. Blå: Fordeling af 1000 gennemsnit af 10 målinger. Grøn: Fordeling af 1000 gennemsnit af 100 målinger.
Frihedsgrader og n
Erfaringsmæssigt er bestemmelsen af antal frihedsgrader (\(f\)) og antal målinger (\(n\)) noget af der der volder vanskeligheder. Følgende uddyber derfor dette:
\(n\) indgår i beregningen af \(SEM\), sammen med \(SD\), og derfor er det nærliggende at tro at der er en sammenhæng mellem disse to størrelser. Det er der ikke! \(n\) er, som nævnt ovenfor, det antal målinger som er brugt til at bestemme gennemsnittet. \(f\) derimod er fastlagt af \(SD\).
Ofte vil \(SD\) og \(n\) være bestemt ved hjælp af den samme stikprøve (f.eks. 10 målinger på en kontrolprøve, som anvendes til at beregne både analyseusikkerheden og gennemsnit - dvs. et gæt på prøvens sande værdi). Her vil der gælde at \(f = n-1\) (se side 4.11). Andre gange vil man imidlertid beregne et gæt på prøvens sande værdi udfra de seneste 10 målinger på en kontrolprøve, mens analyseusikkerheden er bestemt ud fra de sidste mange måneders målinger. Dvs. at spredningen er fastsat med et meget stort antal frihedsgrader (\(f = \infty\)).
Bemærk at de målinger der bruges til at fastlægge \(\overline{x}\) og \(SD\), naturligvis skal stamme fra samme population. Men de behøver altså ikke nødvendigvis at stamme fra samme stikprøve.
Man kan således sagtens beregne et konfidensinterval for et gennemsnit baseret på en enkelt måling (\(n=1\)), hvis blot spredningen er fastsat vha en anden stikprøve med et stort antal frihedsgrader.
Man kan ind i mellem komme ud for at gennemsnittet er bestemt ud fra én stikprøve, mens spredningen er bestemt ud fra en anden stikprøve, som er for lille til at man kan sætte antal frihedsgrader til "uendelig". I dette tilfælde er ovenstående formel til beregning af konfidensintervaller i princippet forkert, men i praksis kan den formentlig anvendes, hvis blot ikke \(f\) er alt for lille. |