Konfidensinterval for middelværdi
Bemærk: Det er ikke strengt nødvendigt at forstå denne side, for at kunne arbejde med konfidensintervaller. Men hvis man gerne vil opnå en mere matematisk forståelse for statistikken er den god at læse. Det kan i øvrigt tilføjes at har man forstået denne side, har man faktisk også forstået indledningen til de statistiske hypotesetest i kapitel 6.
En (lidt) mere matematisk udledning
Betragt en stikprøve fra en normalfordeling med middelværdi \(\mu_0\) og spredning \(\sigma\) - det kunne f.eks. være et antal målinger på en kontrolprøve med den sande værdi \(\mu_0\), hvor den anvendte analyse har en usikkerhed på \(\sigma\).
Stikprøvens gennemsnit betegnes som sædvanlig med \(\overline{x}\), dens spredning med \(SD\) og antallet af målinger i stikprøven betegnes med \(n\).
Nu kan matematikerne bevise at hvis man gentagne gange laver en sådan stikprøve, og hver gang beregner størrelsen:
$$t=\frac{\overline{x}-\mu_0}{SD/\sqrt{n}}$$
så vil denne størrelse være t-fordelt (læs lidt mere om t-fordelingen på side 3.11). Antallet af frihedsgrader for denne t-fordeling er lig med antallet af frihedsgrader for \(SD\) (se side 4.11).
I forbindelse med beregning af konfidensintervaller er hele problemet jo at \(\mu_0\) er ukendt, men ovenstående kan netop anvendes til at vurdere om en given værdi af \(\mu_0\) er "rimelig", og dermed til at beregne et interval som indeholder de "rimelige" værdier af \(\mu_0\).
For at forstå hvad der menes med "rimelig" betragtes igen eksemplet på side 5.3. Gennemsnittet af den observerede stikprøve er:
\[\begin{aligned}
\overline{x}\ &=10{,}04\\
SD\ &=1{,}05\\
n\ &=10
\end{aligned}\]
Herefter kan man spørge: Er det rimeligt at tro at \(\mu_0=10,5\)? Hvis dette er tilfældet så fås:
$$t=\frac{\overline{x}-\mu_0}{SD/\sqrt{n}}=\frac{10{,}04-10{,}5}{1{,}05/\sqrt{10}}=-1,4$$
Som nævnt i starten kan det bevises at hvis 10,5 faktisk er den sande middelværdi, så er denne størrelse t-fordelt, dvs. spørgsmålet kan omformuleres til:
Er det rimeligt at få værdien -1,4 i en t-fordeling med 9 frihedsgrader?
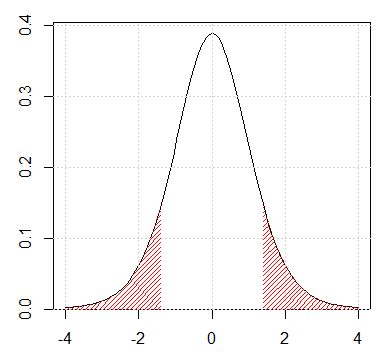
Figur 1: t-fordelingen med 9 frihedsgrader. Arealet af de skraverede områder angiver sandsynligheden for at en tilfældig stikprøve fra en normalfordelt population vil give en t-værdi mindre end -1,4 eller større end 1,4 (p = 0,20).
Ved at betragte figur 1 ses at det ikke ser helt urimeligt ud. Det skraverede areal angiver sandsynligheden for at man får en t-værdi under -1,4 eller over 1,4 og denne sandsynlighed ligger noget over 0,05. En t-værdi på -1,4 forekommer altså jævnligt hvis man udtager en tilfældig stikprøve fra en normalfordelt population.
Hvis man er interesseret i et 95%-konfidensinterval, kan man lidt mere præcist definere de rimelige t-værdier som dem der ligger mellem 0,025- og 0,975-fraktilerne i t-fordelingen. Disse kan beregnes til (se side 13.5) \(t_{0{,}025}(f)=-2{,}262\) og \(t_{0{,}975}(f)=+2{,}262\).
Dette betyder at de værdier af \(\mu_0\) som er i overensstemmelse med den observerede stikprøve er dem som opfylder følgende:
\[\begin{aligned}
&t_{0{,}025}(f) < \frac{\overline{x}-\mu_0}{SD/\sqrt{n}} < t_{0{,}975}(f)\\
\Updownarrow\ & \\
&t_{0{,}025}(f)\cdot \frac{SD}{\sqrt{n}}<\overline{x}-\mu_0 < t_{0{,}975}(f)\cdot \frac{SD}{\sqrt{n}}\\
\Updownarrow\ & \\
&\overline{x}-t_{0{,}975}(f)\cdot \frac{SD}{\sqrt{n}}<\mu_0 < \overline{x}-t_{0{,}025}(f)\cdot \frac{SD}{\sqrt{n}}\\
\Updownarrow\ & \\
&\overline{x}-t_{0{,}975}(f)\cdot \frac{SD}{\sqrt{n}}<\mu_0 < \overline{x}+t_{0{,}975}(f)\cdot \frac{SD}{\sqrt{n}}\\
\end{aligned}\]
(Den sidste linje udnytter at t-fordelingen er symmetrisk dvs. at \(t_{0{,}975}(f) = -t_{0{,}025}(f)\))
Og dermed har man formel (1) på side 5.2. |