Andre fordelinger
Det er sandsynligvis en fordel at vente med at læse denne side, til man for brug for det, i forbindelse med kapitlerne om konfidensintervaller eller hypotesetest.
Formler til beregning af sandsynligheder og fraktiler i nedenstående fordelinger vha. Excel er vist i kapitel 13.
t-fordelingen
Ud over normalfordelingen findes en lang række fordelinger, som er relevante i forskellige sammenhænge. Den første man støder på er typisk t-fordelingen. Mens normalfordelingen er entydigt specificeret af en middelværdi og en spredning, så specificeres t-fordelingen af et enkelt tal der kaldes "frihedsgrader". Figur 1 viser t-fordelingen for frihedsgraderne 2,5 og 100. Man kan bemærke at når antallet af frihedsgrader vokser mod uendelig, så begynder t-fordelingen mere og mere at ligne en normalfordeling (med middelværdi nul og spredning 1).
t-fordelingen dukker op i række sammenhænge som det ses i de følgende kapitler.
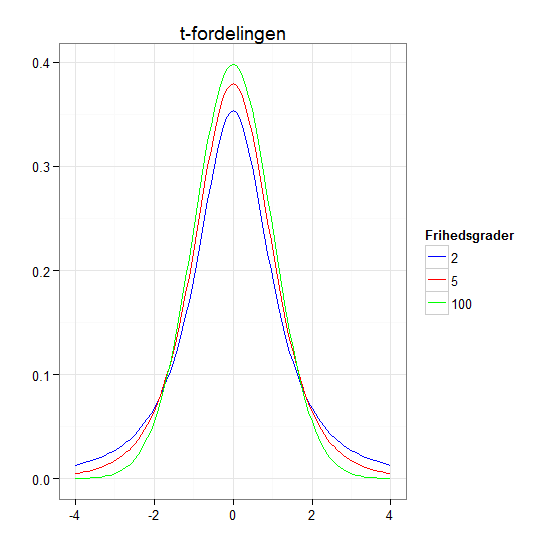
Figur 1: Tæthedsfunktioner for t-fordelinger med hhv. 2, 5 og 100 frihedsgrader
F-fordelingen
F-fordelingen afhænger af 2 forskellige frihedsgrader. Man taler om at F-fordelingen har et antal frihedsgrader for nævneren og et antal frihedsgrader for tælleren. Figur 2 illustrerer 3 forskellige F-fordelinger som alle har samme antal frihedsgrader for tæller og nævner. Ligesom med t-fordelingen kan det bemærkes at når antallet af frihedsgrader vokser, begynder F-fordelingen mere og mere at ligne en normalfordeling. F-fordelingen dukker op, når man betragter forholdet mellem 2 observerede varianser - se f.eks. side 6.14.

Figur 2: Tæthedsfunktioner for 3 F-fordelinger med lige mange frihedsgrader i tæller og nævner.
\(\chi^2\)-fordelingen
\(\chi^2\)-fordelingen dukker op i forbindelse med \(\chi^2\)-testen (sjovt nok), eller i forbindelse med beregning af konfidensintervaller for spredninger. Ligesom t-fordelingen afhænger \(\chi^2\)-fordelingen af antallet af frihedsgrader.

Figur 3: Tæthedsfunktioner for 3 forskellige \(\chi^2\)-fordelinger |