Noter i statistik

Metodesammenligning

Ofte har man brug at foretage en sammenligning af to metoder/apparater, som bruges til den samme analyse. I forhold til forsøgsdesign kan man overordnet anvende to metoder, som hver har sine styrker og svagheder.

• Et parret design, hvor et antal forskellige patientprøver måles èn gang på hvert apparat.
• Et uparret design, hvor èn prøve måles flere gange på hvert apparat.

Parret design

Det typiske valg er formentlig det parrede design. Dette skyldes at man oftest har brug for at sammenligne metoderne i flere forskellige måleniveauer, hvilket lettest gøres med det parrede design. Man kan ikke nødvendigvis antage at blot fordi metoderne stemmer overens i et niveau, så stemmer de overens i alle niveauer.

Ulempen ved det parrede design er, at det er problematisk at anvende en hypotesetest til at foretage sammenligningen. Dette skyldes at den parrede test sammenligner middelværdien af målingerne fra den ene metode med middelværdien af målingerne på den anden metode. At disse middelværdier er identiske, er selvfølgelig ikke tilstrækkeligt til at konkludere at metoderne er identiske. Middelværdierne vil f.eks. kunne blive ens hvis et xy-plot (se side 2.4) med metode 1 på x-aksen og metode 2 på y-aksen ser ud som herunder:

Figur 1: Eksempel på en åbenlyst dårlig sammenhæng mellem 2 metoder, som ikke opdages af en parret test, idet middelværdierne for metode 1 og metode 2 er ens (ca. 5).

Nedenfor under punktet "Bland-Altman plot" diskuteres yderligere hvordan man bør analysere sine data, når man har gennemført en metodesammenligning baseret på et parret design.

Uparret design

I udvalgte situationer kan det være tilstrækkeligt at foretage metodesammenligningen i et niveau. Det kan f.eks. være i den situation hvor analysen udelukkende anvendes til at vurdere om en koncentration ligger over eller under en bestemt cut-off grænse (eksempelvis glucose til diagnostik af diabetes).

I så fald anskaffer man, på den ene eller anden måde, en prøve med en koncentration omkring denne cut-off grænse, måler prøven et passende antal gange på hver apparat, og sammenligner resultaterne vha. en uparret test. På side 7.2 er en nærmere diskussion af hvor mange målinger man bør foretage, hvis man vælger dette design.

Ulempen ved dette design er som nævnt at man kun kan foretage sammenligningen i et niveau. Metoden kan eventuelt gentages i flere forskellige niveauer, men i så fald bliver der principielt tale om multiple tests, hvilket også er problematisk, jævnfør diskussionen på side 6.16. Denne mulighed diskuteres yderligere i forbindelse med holdbarhedsforsøget på næste side (teknisk skal man i så fald bruge en tosidet variansanalyse med gentagelser - se side 6.18).

Bland-Altman plot

I 1983 publicerede D. G. Altman og J. M. Bland en artikel¹ hvor de diskuterer metodesammenligning baseret på et parret design. I denne artikel afvises de fleste beregningsbaserede metoder (hypotesetest, regression og korrelation), og i stedet beskriver de, at den mest fornuftige (og måske eneste brugbare) metode, er fremstilling af et differensplot (se side 2.5) og eventuelt et xy-plot (side 2.4). 

Bland og Altman foretrækker et differensplot, som indenfor sundhedsvidenskab derfor også kaldes et "Bland-Altman" plot. 

Herunder vises en række sammenhørende differensplot, og det gennemgås hvad man skal kigge efter, når man vurderer dem. 

Eksempel 1

På differensplottet i eksempel 1 ses ingen tendens til, at forskellen mellem apparat 1 og 2 afhænger af koncentrationen, ligesom der heller ikke er tegn på at analyseusikkerheden varierer. Dette ville i givet fald afspejle sig i, at differencerne begyndte at sprede sig mere og mere omkring deres middelværdi. 

I dette tilfælde er det således principielt muligt at anvende en hypotesetest til at undersøge om de to apparater måler forskelligt. Man bør kunne antage at differencerne er normalfordelte, da der ikke er andre effekter end apparaternes tilfældige variation, og da denne ser ud til at være uafhængig af koncentrationen. Man bør derfor kunne anvende en t-test.

Spørgsmålet er så om det er nødvendigt at bruge en t-test. Med dette konkrete differensplot er der ingen tvivl om, at der er en systematisk forskel mellem apparaterne, men i andre tilfælde kan det være vanskeligt at afgøre udfra differensplottet; og så kan en t-test naturligvis være berettiget. 

Eksempel 2

I dette eksempel er der ligeledes heller ikke tegn på at analyseusikkerehden varierer med værdien. Til gengæld er det oplagt, at forskellen mellem de to apparater afhænger af niveauet. Ved lave koncentrationer ser de ud til at stemme overens, mens apparat 2 måler højest ved højere koncentrationer. I denne situation giver det ikke mening at bruge en hypotesetest, da forskellen mellem de to apparater afhænger af måleniveauet, hvilken t-testen ikke kan tage højde for. 

Eksempel 3

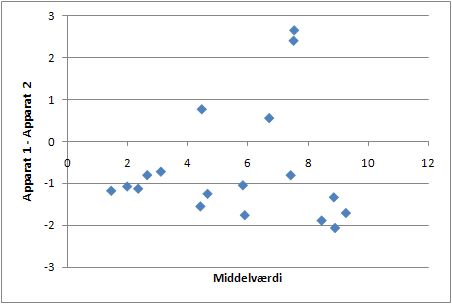
Dette plot afslører den - meget normale - situation af apparaternes analyseusikkerhed afhænger af niveauet. Dette ses ved at differencerne begynder at sprede mere og mere, når man bevæger sig til højre på grafen. Også i denne situation kan det være problematisk at anvende en hypotesetest. F.eks. risikerer man at den rimeligt tydelige systematiske forskel der er i det lave niveau, vil drukne i den meget store tilfældige variation som ses i det høje niveau. 

Hvad skal man IKKE gøre

Ifølge Bland og Altman afslører et xy-plot sjældent noget, som man ikke kan se i et differensplot. Ikke desto mindre ses disse plot i litteraturen, og det er formentlig helt uproblematisk. Derudover ses det, at man tager skridtet videre, og beregner enten en korrelationskoefficient eller liniær regression, og forsøger at bruge dette til at sige noget om sammenhængen mellem de to apparater. 

I mange sammenhænge er korrelation og regression vigtige (eller decideret uundværlige) redskaber, men i forhold til en sammenligning af to apparater som foretager identiske analyser, er det oftest meningsløst.

Korrelationskoefficienten er uinteressant af to grunde: 

1. En metodesammenligning har til formål at undersøge om der er en systematisk forskel mellem to apparater. En systematisk forskel påvirker imidlertid ikke korrelationskoefficienten. Den analytiske variation på apparaterne vil påvirke korrelationskoefficienten, men dette er til gengæld ikke relevant når man skal sammenligne apparaternes korrekthed.
2. Hvis sammenligningen foretages vha. prøver som ligger tæt på hinanden (i forhold til analyseusikkerheden) vil man automatisk få en lav korrelationskoefficient - bemærk at dette må betragtes som et dårligt forsøgsdesign, hvis målet er at undersøge hele måleområdet. Og omvendt får man automatisk en høj korrelationskoefficient, hvis man anvender prøver som ligger "langt fra" hinanden. 

Lineær regression er ligeledes problematisk af flere grunde: 

1. Almindelig lineær regression har som forudsætning, at man kan tale om en uafhængig parameter, og at denne er fastlagt uden nogen usikkerhed. Dette er aldrig opfyldt i forbindelse med en apparatsammenligning. (Denne indvending gælder faktisk også korrelationskoefficienten).
2. Alternativt kan man så anvende regressionsmetoder som ikke har ovennævnte forudsætning. Disse er imidlertid komplicerede at anvende hvis man ikke har adgang til specialiseret software; i særdeles hvis man også skal teste om den fundne hældning er signifikant forskellig fra 1 (og skæringen er signifikant forskellig fra 0). 

Referencer

1. Altman DG, Bland JM: "Measurement in Medicine: the Analysis of Method Comparison studies", The Statistician 32 (1983) 307-317