Mere om lineær regression
Lineær sammenhæng
Først og fremmest er det væsentligt at forstå hvad der menes, når man taler om at der skal være en lineær sammenhæng mellem to variable (\(x\) og \(y\)).
Hvis man har et sæt bestående af \(n\) sammenhørende målinger \((x_i,y_i)\) hvor \(i = 1,2, \ldots ,n\), så er den matematiske betydning, i denne sammenhæng, at der skal gælde følgende sammenhæng mellem \(x\) og \(y\):
\[\begin{equation}\label{ref1}
y_i=a + b\cdot x_i + \epsilon_i
\end{equation}\]
Ovenstående ligning betyder at der "i gennemsnit" er en linæer sammenhæng mellem \(x\) og \(y\), men derudover er hver måling behæftet med tilfældig fejl (\(\epsilon_i\)). Det vigtige er at disse fejl er normalfordelt med en spredning som er uafhængig af værdien af \(x\). Det er altså ikke et krav at alle de observerede punkter ligger præcist på en ret linje, men den måde de afviger fra en ret linje på, skal være tilfældig.
Denne graf viser en situation som opfylder ovenstående:

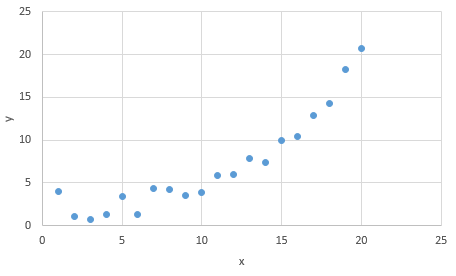
Hvorimod nedenstående graf viser en situation hvor det tydeligvis ikke giver mening at bruge lineær regression, idet den "gennemsnitlige" sammenhæng mellem \(x\) og \(y\) ikke er lineær:
Residualer
Selv om de tekniske aspekter af lineær regression på side 2.11 blev overladt til Excel, er det forholdvist enkelt at forstå det grundlæggende princip bag almindelig lineær regression.
De røde streger på figur 1, viser de såkaldte residualer, dvs. forskellen mellem de observerede \(y\)-værdier, og de estimerede værdier (den grønne streg). Bemærk at de røde streger næsten svarer til fejlene (\(\epsilon_i\)) i ligning \(\ref{ref1}\), men også kun næsten. \(\epsilon_i\) angiver fejlen på den i'te måling i forhold til den sande sammenhæng mellem \(x\) og \(y\) (som man jo typisk ikke kender), mens residualerne angiver fejlen målt i forhold til den estimerede sammenhæng mellem \(x\) og \(y\).
Regressionslinjen beregnes som den linie der minimerer størrelsen af disse residualer (eller mere præcist: summen af kvadratet på residualerne).
Denne metode har principielt nogle forudsætninger, hvoraf nedenstående nok er de vigtigste:
- Den uafhængige variabel (\(x\)) skal være bestemt uden usikkerhed
- Den afhængige variabel (\(y\)) skal være normalfordelt - dvs. at hvis man måler flere gange for samme værdi af \(x\), skal disse målinger være normalfordelte. Dette er blot en anden formulering af at fejlene i ligning \(\ref{ref1}\) skal være normalfordelte.
- Og så skal den gennemsnitlige sammenhæng mellem \(x\) og \(y\) selvfølgelig være en ret linje.
Især den første forudsætning er sjældent opfyldt i praksis. Den anden forudsætning medfører desuden at enkelte "outliers" (dvs. punkter som er målt meget forkert) kan påvirke resultatet kraftigt.
Passing-Bablok og Deming regression
Hvis den første forudsætning åbenlyst ikke er opfyldt, men man stadig forventer at de involverede parametre er normalfordelte, så kan man i stedet anvende den såkaldte Deming-regression. Denne metode har som forudsætning at usikkerheden på de to parametre er uafhængig af måleniveauet, og at forholdet mellem de tilsvarende spredninger er kendt.
Hvis ingen af ovennævnte forudsætninger er opfyldt, kan man anvende såkaldt Passing-Bablok-regression. Begge former for regression er komplicerede at udføre, og kan i praksis kun anvendes, hvis man har adgang til passende statistisk software. De bliver derfor ikke behandlet nærmere her, men det er relevant at kende til deres eksistens; bla. fordi de ofte anvendes i litteraturen. Hvis man har behov for at lave Deming- eller Passing-Bablok-regression kan OpenSource-programmet "R" anbefales. Der findes to udvidelsespakker ("mcr" og "MethComp") som begge kan udføre beregningerne.
|