Beregning i normalfordelingen
Overordnet har man i statistik brug for at kunne beregne enten sandsynligheder eller fraktiler (genlæs eventuelt side 3.3). Hvis man ved at populationen er normalfordelt, er dette relativt simpelt, og gennemgås nedenfor vha. et par eksempler. Bemærk at hvis man bruger moderne software (Excel eller lignende, så kan disse beregninger typisk laves endnu nemmere end gennemgået på denne side).
Beregning af fraktiler
Betragt B-hæmoglobin, stofk. hos raske mænd. Denne parameter er normalfordelt med middelværdi \(\mu=9{,}25 \text{ mmol/L}\) og spredning \(\sigma=0{,}6\text{ mmol/L}\). Man ønsker nu at bestemme den hæmoglobinkoncentration som er kendetegnet ved at 2,5% af alle raske mænd har en værdi der er lavere - eller med andre ord: 0,025-fraktilen.
Den normerede normalfordeling
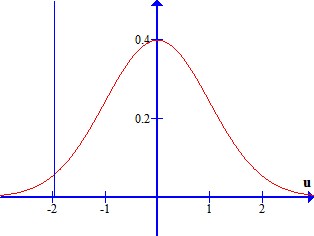
Opgaven løses enten ved tabelopslag eller ved beregning i f.eks. Excel. Ved tabelopslag findes der (selvfølgelig) ikke tabeller over alle normalfordelinger, men kun over normalfordelingen med middelværdi 0 og spredning 1. Dette er den såkaldt normerede normalfordeling. I denne fordeling kan man (vha. tabel 2 på side 13.6) finde ud af at 0,025-fraktilen er \(u = -1{,}96\).
 |
 |
| Den normerede normalfordeling |
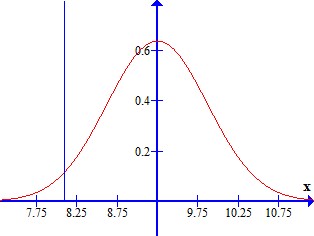
Hæmoglobinkoncentrationen hos raske mænd |
| De tynde lodrette blå streger repræsenterer 0,025-fraktilerne i begge fordelinger. Oversættelsen fra den ene fordelingen til den anden foregår vha. formlen \(x=\mu+u\cdot\sigma\), hvor \(x\) er fraktilen i hæmoglobinfordelingen, mens \(u\) er fraktilen i den normerede normalfordeling |
Denne fraktil kan man nu omregne til den tilsvarende 0,025-fraktil i hæmoglobinfordelingen vha. formlen (husk at 0,025-fraktilen i den normerede fordeling er -1,96):
\[\begin{aligned}
x &=\mu+u\cdot \sigma \\
&=9{,}25 \text{ mmol/L}-1{,}96\cdot 0{,}6 \text{ mmol/L}\\
&=8{,}1 \text{ mmol/L}
\end{aligned}\]
dvs at 2,5% af alle raske mænd har en hæmoglobinkoncentration som er under 8,1 mmol/L.
Beregning af sandsynligheder
Hvis man skal beregne en sandsynlighed - f.eks. sandsynligheden for at en tilfældig rask mand har en B-hæmoglobin, stofk. under 9,50 mmol/L - så er fremgangsmåden lige modsat af fraktil-beregningen.
Først skal man oversætte problemet til at bestemme en sandsynlighed i den normerede normalfordeling, dvs. man skal finde den fraktil (\(u\)) i den normerede normalfordeling som svarer til 9,50 mmol/L i den interessante fordeling. Dette gøres blot ved at isolere \(u\) i den formel der blev anvendt ovenfor, dvs:
\[\begin{aligned}
u &=\frac{x-\mu}{\sigma}\\
&=\frac{9{,}50 \text{ mmol/L}-9{,}25\text{ mmol/L}}{0{,}6 \text{ mmol/L}}\\
&=0{,}42
\end{aligned}\]
Herefter kan man nu slå sandsynligheden op i tabel 1 på side 13.6, ved at slå op under den beregnede værdi for \(u\). Dvs. man får at:
$$P(X<9{,}50\text{ mmol/L}) = \Phi(0{,}42) = 0{,}6628 = 66{,}28\%$$
Bemærk notationen \("\Phi(0{,}42)"\). Dette er en speciel notation som nogen gange anvendes som forkortelse for \("P(X < 0{,}42)"\) når beregningen skal foretages i den normerede normalfordeling. |