\(P_{fr}\) og \(P_{ed}\)
To størrelser er væsentlige i forbindelse med udarbejdelse af et program til kvalitetskontrol af en analyse. Nemlig sandsynligheden for at kontrollen kan opdage hvis analysen begynder at give forkerte resultater, samt sandsynligheden (risikoen) for at kontrollen giver en alarm selv om analysen fungerer korrekt. Førstnævnte sandsynlighed betegnes \(P_{ed}\) (Probability or error detection) og sidstnævnte \(P_{fr}\) (probability of false rejection).
Det er værd at bemærke at hvis man sammenligner kvalitetskontrol med en statistisk hypotesetest, hvor nul-hypotesen naturligvis svarer til at analysen ikke er behæftet med fejl, så er begreberne \(P_{fr}\) og \(P_{ed}\) fuldstændigt analoge med type 1 fejlen hhv. teststyrken (eller 1 minus type 2 fejlen) - som gennemgået på side 6.4.
Præcis som med teststyrken for en hypotesetest, er det ved beregning af \(P_{ed}\) nødvendigt at specificere størrelsen og typen af den fejl man ønsker at opdage. Skred i analysens korrekthed angives med \(\Delta SE\) (systematic error) og angives ofte i enheder af \(\sigma_{ana}\) (altså den analyseusikkerhed der anvendes til at fremstille kontrolkortet). Ændringer i analysens præcision angives med \(\Delta RE\) (relative error), som angiver forholdet mellem den spredning der udtrykker den aktuelle (forøgede) præcision og \(\sigma_{ana}\).
Eksempel
\(P_{fr}\)
Betragt en kontrolprocedure bestående af en enkelt kontrolregel, nemlig 13s. Dvs. at kontrollen forkastes hvis kontrolmålingen giver en værdi som er mere end \(3 \cdot \sigma_{ana}\) fra dens sande værdi (\(\mu\)). Under den antagelse at analysen fungerer korrekt, er kontrolmålingerne altså normalfordelt med middelværdi \(\mu\) og spredning \(\sigma_{ana}\) . Dermed bliver sandsynligheden for en falsk forkastelse af kontrollen:
$$P_{fr} = P(X< \mu-3\cdot \sigma_{ana})+ P(X> \mu+3\cdot \sigma_{ana})=2 \cdot \Phi(-3)=0{,}0026 = 0{,}26\%$$
Det andet lighedstegn ovenfor er forklaret på side 3.3 formel 1 og 2, samt afsnittet "beregning af sandsynligheder" på side 3.12. Tredje lighedstegn er blot en sandsynlighedsberegning som vist på side 13.6.
Denne kontrolprocedure vil altså 1 ud af 400 gange resultere i en falsk forkastelse, hvilket formentlig er acceptabelt i de fleste situationer.
\(P_{ed}\)
For at beregne \(P_{ed}\) er det som nævnt nødvendigt at specificere den fejl man ønsker at kunne opdage. Denne specifikation bør naturligvis tage udgangspunkt i de kliniske krav til analysen. Specifikationen foretages oftest relativt den analyseusikkerheden. Hvis man f.eks. ønsker at kunne opdage et skred i analysens korrekthed på \(2 \cdot \sigma_{ana}\) specificeres dette som:
$$\Delta SE = 2s$$
Ønsker man at kunne opdage en tredobling af analyseusikkerheden specificeres dette som:
$$\Delta RE= 3s$$
Bestemmelse af teststyrken kan i simple tilfælde (som dette) foretages ved beregning. Ved kontrolprocedurer som er sammensat af flere forskellige kontrolregler, eller ved mere komplicerede kontrolregler, bliver det imidlertid hurtigt kompliceret (eller umuligt) at foretage disse beregninger. Det nemmeste er derfor at have adgang til et computerprogram som kan foretage beregningerne, eller at finde et såkaldt styrkediagram. Disse kan bl.a. findes i litteraturen, f.eks. i denne artikel: "Westgard JO, Groth T. Power functions for statistical control rules. Clin Chem 1979;25:863-69.".
Styrkediagrammer for 13s-reglen er vist her:
Ovenstående viser kontrolreglens styrke i forbindelse med skred i korrektheden, dvs. hvis der optræder systematiske fejl. Styrken ved \(\Delta SE = 2s\) kan aflæses til ca. 0,15 eller 15%, dvs. der vil i middel gå ca. 7 dage før denne kontrolregel fanger et sådant skred (hvis man kører 1 kontrol om dagen). Om dette er acceptabelt afhænger igen af de kliniske forhold. Hvis et skred i analysens korrekthed på 2 analyseusikkerheder kan medføre alvorlige gener for patienterne, er det næppe acceptabelt, og man må så gøre noget for at øge kontrolprocedurens styrke. Dette kan være at køre flere kontroller om dagen, eller at medtage andre kontrolregler. I alle tilfælde er prisen naturligvis at Pfr øges. Kan man acceptere et skred på 5 analyseusikkerheder er styrken meget tæt på 1, og i dette tilfælde er der derfor ingen grund til at indføre andre kontrolregler.
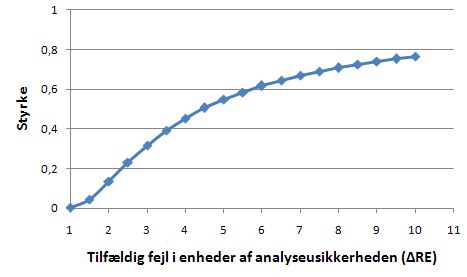 Ovenstående figur viser styrken ved ændring i analysens præcision. Ved en 3-dobling af analyseusikkerheden kan man aflæse at styrken er ca. 0,3, dvs. at denne ændring i middel vil blive opdaget i løbet af et par dage.
Bemærk at \(P_{fr}\) kan aflæses på begge disse grafer, som skæringen med y-aksen, idet \(P_{fr}\) jo netop er sandsynligheden for at "opdage en fejl" i det tilfælde hvor analysen fungerer korrekt. |