Kritisk forskel
(Efter note af Ph.d. Troels Wind)
Analysesvar oplyses i mange tilfælde uden usikkerhed, simpelthen fordi denne ikke spiller en rolle for den kliniske fortolkning af svaret. Fortolkningen vil typisk bestå i en sammenligning med et passende referenceinterval; er analysesvaret indenfor normalområdet eller ej?
Denne side omhandler en situation, hvor usikkerheden på analysesvaret kan have en betydning for den kliniske fortolkning, nemlig hvis det skal afgøres, om analyseresultaterne tyder på en reel ændring i patientens tilstand.
En typisk situation kunne være, at patienten er i et behandlingsforløb, hvor man bl.a. ud fra jævnlige analyser vurderer, om forløbet har den ønskede effekt eller ej. Hvis man i den situation ser en ændring i analysesvaret må man vurdere, om denne ændring er statistisk signifikant - altså om ændringen skyldes andet end tilfældigheder - før man drager en konklusion om hvorvidt behandlingsforløbet har den ønskede effekt.
Den mindste signifikante forskel mellem to analysesvar kaldes den kritiske forskel og angives ofte som relativ ændring i procent. Hvordan kritisk forskel kan beregnes illustreres med udgangspunkt i følgende eksempel.
Eksempel
Hos en mandlig patient der er i behandling for anæmi, har man målt B-Hæmoglobin, stofk. før og efter et behandlingsforløb med følgende resultater:
| Tidspunkt |
B-hæmoglobin, stofk. (mmol/L) |
| Før behandling |
5,5 |
| Efter behandling |
7,4 |
Som referenceinterval for B-Hæmoglobin, stofk. benyttes 8,0 – 10,5 mmol/L.
Ændringen i B-Hæmoglobin, stofk. tyder på, at patienten er i bedring mht. anæmi, men dog ikke helt rask. Den absolutte ændring i B-Hæmoglobin, stofk. er på 1,9 mmol/L, svarende til en relativ ændring på
1,9/5,5 = 0,35 = 35%
Spørgsmålet er, om denne ændring skyldes en effekt af behandlingen, eller blot stammer fra den analytiske variation og/eller den intra-individuelle biologiske variation, der altid optræder i forbindelse med en analyse? Eller med andre ord: Er ændringen statistisk signifikant? Hvorledes dette kan besvares gennemgås herunder.
Princippet
I det følgende betegnes den observerede forskel mellem de to målinger med \(d\). Princippet kan forstås vha. nedenstående figur 1, som viser hvordan \(d\) fordeler sig (hvis man forestiller at man gentager forsøget mange gange), under den antagelse at der ikke er nogen systematisk ændring i patientens tilstand - dvs. at en observeret forskel mellem de to målinger kun skyldes tilfældig variation.
Under denne antagelse er \(d\) normalfordelt med middelværdi nul og en spredning som benævnes \(SD_d\), altså usikkerheden på \(d\). I næste afsnit forklares hvorledes \(SD_d\) beregnes. Ved at kigge på figuren - og eventuelt genlæse side 3.12 - indses det, at \(d\) med 95% sandsynlighed ligger mellem \(-1{,}96\cdot SD_d\) og \(+1{,}96\cdot SD_d\) som markeret af de røde streger. Hvis \(d\) ligger i dette interval, er det altså en rimelig antagelse, at der ikke er en reel forskel på de to målinger.
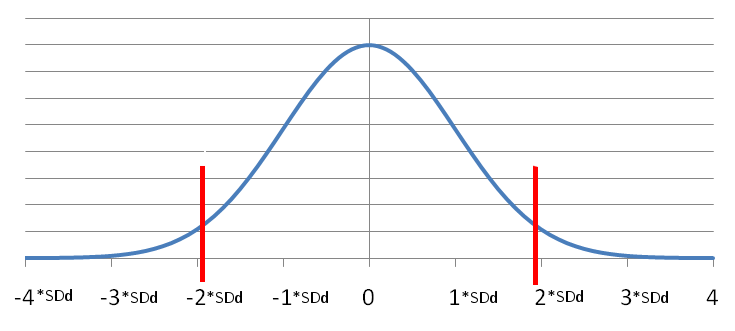
Figur 1: Den distribution der beskriver fordelingen af d hvis der ikke er nogen systematisk forskel på de to målinger. De røde streger markerer intervallet \(\pm1{,}96\cdot SD_d\)
I modsat fald tyder det på at der faktisk er en systematisk forskel på de to målinger, og at den fordeling der beskriver d, derfor ikke ser ud som i figur 1 (alternativt kan man selvfølgelig have været "uheldig" og fået en værdi udenfor stregerne, selv om der kun optræder tilfældig variation - men denne mulighed ignorerer man når man laver statistik).
Bemærk at logikken bag ovenstående principielt er den samme, som ved de hypotesetest der gennemgås i kapitel 6. I dette tilfælde er teststørrelsen blot mere simpel end ved de egentlige hypotesetest.
Kort formulereret gælder der altså at:
\[\begin{equation}
|d|>1{,}96\cdot SD_d \Rightarrow \text{Der er en statistisk signifikant forskel på de to målinger}
\end{equation}\]
Usikkerheden på d
Tilbage er at beregne størrelsen SDd, der er usikkerheden på den absolutte ændring d. Ændringen beregnes som differensen mellem to analysesvar, så først er det nødvendigt at kende usikkerheden på ét analysesvar, SDsvar. Der er to bidrag til denne usikkerhed: Den totale måleusikkerhed (SDmåle) (se nærmere på side 4.12) og den intra-individuelle biologiske variation (SDbio).
Den samlede usikkerhed på et analysesvar beregnes på samme måde som på side 4.12, dvs.
$$SD_{svar}=\sqrt{SD_{måle}^2+SD_{bio}^2}$$
Denne usikkerhed bidrager to gange til SDd, da d beregnes ud fra to svar, og et udtryk for SDd kan nu udledes på følgende måde:
$$\begin{equation}\begin{aligned}
SD_{d}&=\sqrt{SD_{svar}^2+SD_{svar}^2}\\
&=\sqrt{2}\cdot SD_{svar}\\
&=\sqrt{2}\cdot\sqrt{SD_{måle}^2+SD_{bio}^2}
\end{aligned}\end{equation}$$
Ved at kombinere Ligning 1 og Ligning 2 får vi nu at
\[\begin{equation}\begin{aligned}
\lvert d \rvert&>1{,}96\cdot \sqrt{2}\cdot \sqrt{SD_{måle}^2+SD_{bio}^2}\\
&=2{,}77 \cdot \sqrt{SD_{måle}^2+SD_{bio}^2}\\
&\Rightarrow \text{Ændringen er signifikant}
\end{aligned}\end{equation}\]
Fra Ligning 3 kan man se, at den mindste absolutte ændring, der er signifikant, er
\[\begin{equation}
d_{kritisk}=2{,}77 \cdot \sqrt{SD_{måle}^2+SD_{bio}^2}
\end{equation}\]
Af praktiske årsager angives den kritiske forskel som den mindste relative ændring, der er signifikant, og det følger af Ligning 4 at denne kan beregnes som
\[\begin{equation}
\text{Kritisk forskel}=2{,}77 \cdot \sqrt{CV_{måle}^2+CV_{bio}^2}
\end{equation}\]
På akkrediterede laboratorier er måleusikkerheden beregnet for alle analyser og kan findes i laboratoriets dokumenthåndbog. Bud på den intra-individuelle biologiske variation \(CV_{bio}\) kan for de fleste komponenter findes i databasen https://biologicalvariation.eu/meta_calculations. Bemærk at der altid er store usikkerheder på opgørelser af biologisk variation.
Eksempel - fortsat
For analysen B-Hæmoglobin, stofk. fra ovenstående eksempel gælder, at den relative måleusikkerhed er 0,017 (1,7%). Den relative intra-individuelle biologiske variation antages at være 0,028 (2,8%). Den kritiske forskel kan nu beregnes ved hjælp af Ligning 5. |